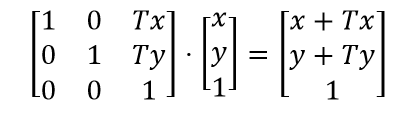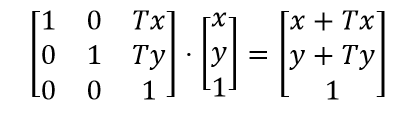#805 – Some Examples of Transform Strings

You can represent any arbitrary matrix transform in XAML using a simple string which includes the values of the elements of the matrix used to do the transformation.  The format is: “M11, M12, M21, M22, OffsetX, OffsetY”.

You can therefore specify any of the standard transforms by also using a simple string in XAML and setting the proper matrix elements.  Here are examples of how to do each of the basic transform types using a simple string:

Scale Transforms: “ScaleX, 0.0, 0.0, ScaleY, 0.0, 0.0”

Rotation transforms: “cos(angle), sin(angle), -sin(angle), cos(angle), 0.0, 0.0”

Translation transforms: “1.0, 0.0, 0.0, 1.0, OffsetX, OffsetY”

Skew transforms: “1.0, tan(SkewY), tan(SkewX), 1.0, 0.0, 0.0”

#800 – Transforms Do Not Affect ActualWidth and ActualHeight

Transforms do not change the values of the original element’s dimensions, as reported by the ActualWidth and ActualHeight properties.  This is true for both LayoutTransforms and RenderTransforms.

    <StackPanel>
        <Button Name="btn1" Content="Apollo" HorizontalAlignment="Center"
                Margin="5"/>

        <Button Name="btn2" Content="Apollo" HorizontalAlignment="Center"
                Margin="5">
            <Button.RenderTransform>
                <ScaleTransform ScaleX="1.5" ScaleY="2.0"/>
            </Button.RenderTransform>
        </Button>

        <Button Name="btn3" Content="Apollo" HorizontalAlignment="Center"
                Margin="5">
            <Button.LayoutTransform>
                <ScaleTransform ScaleX="1.5" ScaleY="2.0"/>
            </Button.LayoutTransform>
        </Button>

        <Button Content="Debug" Click="Button_Click" HorizontalAlignment="Center"
                Margin="10"/>
    </StackPanel>

Notice that when we inspect the elements in the debugger, they all have identical values for ActualWidth and ActualHeight.

#799 – How Transforms Are Combined

Because all transforms in WPF use homogeneous coordinates, combining transforms is accomplished simply by multiplying one or more 3 x 3 matrices together.

For example, suppose that we want to combine a rotation and a translation transform:

                <TransformGroup>
                    <RotateTransform Angle="30"/>
                    <TranslateTransform X="5.0" Y="10.0"/>
                </TransformGroup>

Recall that the 3 x 3 transformation matrix for rotation looks like:

And recall that the 3 x 3 transformation matrix for translation looks like:

To combine these two transforms together, we multiply the matrices, but in the opposite order from how they are listed:

For the example above, that works out to:

Multiplying any point by this final matrix will result in the point first being rotated and then translated.

In WPF, all of this works automatically behind the scenes.  You just specify in XAML the transforms that you want applied to your user interface elements and WPF calculates and stores the proper transformation matrix.

#796 – WPF Transforms Use Homogeneous Coordinates

We saw that we can perform scale and rotation transforms on points in 2D by multiplying a 2 x 2 transformation by a 2 x 1 matrix representing a point.  A translation transform, however, could not be accomplished using a 2 x 2 matrix.  Instead, we multiply a 3 x 3 matrix by a 3 x 1 matrix that represents the 2D point.

In WPF, all 2D transforms are accomplished using a 3 x 3 transformation matrix and a 3 x 1 point matrix.  The 3 x 1 matrix contains the x and y components of the point in the first two rows and a value of 1 as the third row.  This is done so that we can easily combine scale, rotate and translation transforms, since they all use matrices of the same dimensions.

In representing a 2D point using a 3 x 1 matrix, WPF is making us of homogeneous coordinates, which involves adding a third dimension, represented by the third row of the point matrix.